Subsection 4.6.2 How to Eulerize
¶Not every graph has an Euler path or circuit, yet in some situations we will need to complete a circuit in a graph. In order to do that, we will need to reuse some edges. To indicate this, we will duplicate certain edges in the graph until an Euler circuit exists.
Definition 4.6.4 Eulerization
Eulerization is the process of adding edges to a graph to create an Euler circuit on a graph. To eulerize a graph, edges are duplicated to connect pairs of vertices with odd degree. Connecting two odd degree vertices increases the degree of each, giving them both even degree. When two odd degree vertices are not directly connected, we can duplicate all edges in a path connecting the two.
Note that we can only duplicate edges, not create edges where there wasn’t one before. Duplicating edges would mean walking or driving down a road twice, while creating an edge where there wasn’t one before is akin to installing a new road!
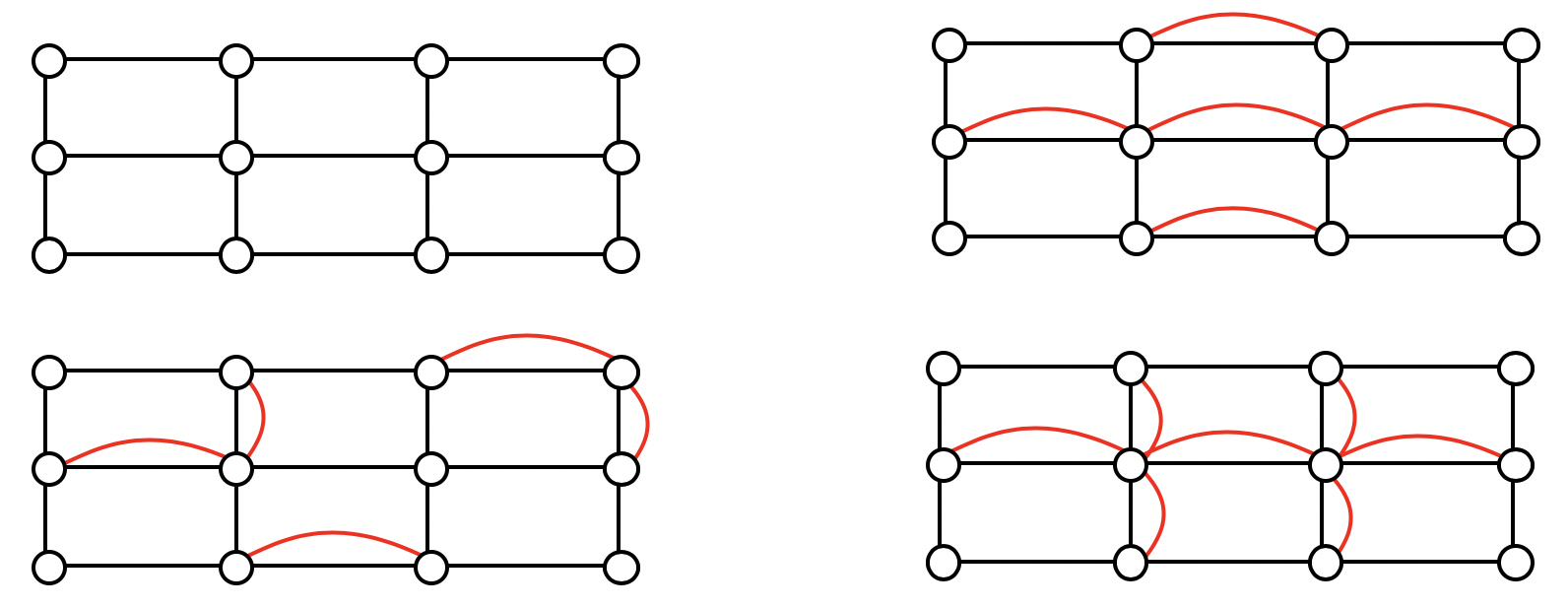
Example 4.6.5
For the rectangular graph shown, three possible eulerizations are shown. Notice in each of these cases the vertices that started with odd degrees have even degrees after eulerization, allowing for an Euler circuit.
In the example above, you’ll notice that the last eulerization required duplicating seven edges, while the first two only required duplicating five edges. If we were eulerizing the graph to find a walking path, we would want the eulerization with minimal duplications. If the edges had weights representing distances or costs, then we would want to select the eulerization with the minimal total added weight.
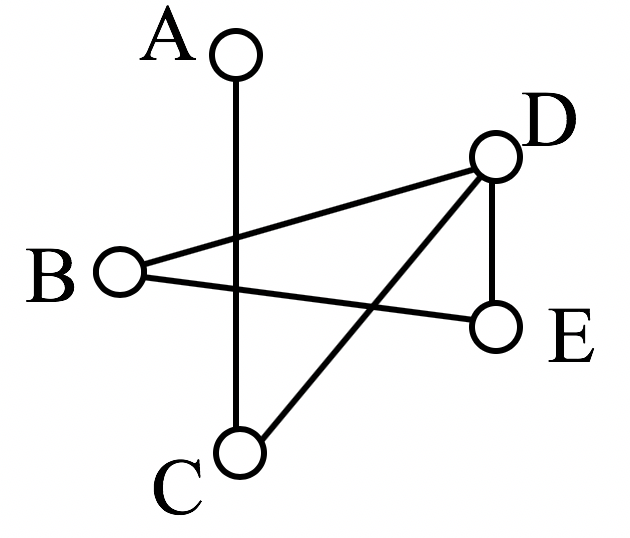
Try it Now 4.6.6
Eulerize the graph shown, then find an Euler circuit on the eulerized graph.
The problem of finding the optimal eulerization is called the Chinese Postman Problem, a name given by an American in honor of the Chinese mathematician Mei-Ko Kwan who first studied the problem in 1962 while trying to find optimal delivery routes for postal carriers. This problem is important in determining efficient routes for garbage trucks, school buses, parking meter checkers, street sweepers, and more.