Algorithm 4.8.1 Brute Force Algorithm (a.k.a. exhaustive search)
- List all possible Hamiltonian circuits.
- Find the length of each circuit by adding the edge weights.
- Select the circuit with minimal total weight.
Assuming a weighted graph has a Hamiltonian circuit, how can we find the most efficient one? That is, the circuit with the smallest weight. This turns out to be a very hard problem.
Finding a shortest Hamiltonian circuit on a weighted graph is called the Traveling salesman problem (TSP) because the question can be framed like this: Suppose a salesman needs to give sales pitches in four cities. He looks up the airfares between each city, and puts the costs in a graph. In what order should he travel to visit each city once then return home with the lowest cost?
To answer this question of how to find the lowest cost Hamiltonian circuit, we will consider some possible approaches. The first option that might come to mind is to just try all different possible circuits.
Apply the Brute force algorithm to find the minimum cost Hamiltonian circuit on the graph below.

To apply the Brute force algorithm, we list all possible Hamiltonian circuits and calculate their weight:
| Circuit | Weight |
| ABCDA | 4+13+8+1 = 26 |
| ABDCA | 4+9+8+2 = 23 |
| ACBDA | 2+13+9+1 = 25 |
Note: These are the unique circuits on this graph. All other possible circuits are the reverse of the listed ones or start at a different vertex, but result in the same weights.
From this we can see that the second circuit, ABDCA, is the optimal circuit.
The Brute force algorithm is optimal; it will always produce the Hamiltonian circuit with minimum weight. Is it efficient? To answer that question, we need to consider how many Hamiltonian circuits a graph could have. For simplicity, let’s look at the worst-case possibility, where every vertex is connected to every other vertex -- that is, a complete graph.
Suppose we had a complete graph with five vertices like the air travel graph above. From Seattle there are four cities we can visit first. From each of those, there are three choices. From each of those cities, there are two possible cities to visit next. There is then only one choice for the last city before returning home. That is a total of \(4\cdot 3\cdot 2\cdot 1\) or \(24\) routes. Half of these are duplicates in reverse order, so that leaves \(12\) routes
This doesn't seem unreasonably huge, but consider what happens as the number of cities increases. If there are \(20\) cities there will be \(60,822,550,204,416,000\) unique routes to check. If a computer looked at one billion circuits a second, it would still take almost two years to examine all the possible circuits with only 20 cities! Certainly Brute Force is not an efficient algorithm.
Unfortunately, no one has yet found an efficient and optimal algorithm to solve the TSP, and it is very unlikely anyone ever will. Since it is not practical to use brute force to solve the problem, we turn instead to heuristic algorithms; efficient algorithms that give approximate solutions. In other words, heuristic algorithms are fast, but may or may not produce the optimal circuit.
Consider our earlier graph, shown to the right. Starting at vertex A, the nearest neighbor is vertex D with a weight of 1. From D, the nearest neighbor is C, with a weight of 8. From C, our only option is to move to vertex B, the only unvisited vertex, with a cost of 13. From B we return to A with a weight of 4.

The resulting circuit is ADCBA with a total weight of 1+8+13+4 = 26.
We ended up finding the worst circuit in the graph! What happened? Unfortunately, while it is very easy to implement, the NNA is a greedy algorithm, meaning it only looks at the immediate decision without considering the consequences in the future. In this case, following the edge AD forced us to use the very expensive edge BC later.
As an alternative, our next approach will step back and look at the “big picture” – it will select first the edges that are shortest, and then fill in the gaps.
Repeat step 1, adding the cheapest unused edge to the circuit, unless:
Using the four vertex graph from earlier, we can use the Sorted Edges algorithm.
The cheapest edge is AD, with a cost of 1. We highlight that edge to mark it selected.
The next shortest edge is AC, with a weight of 2, so we highlight that edge.
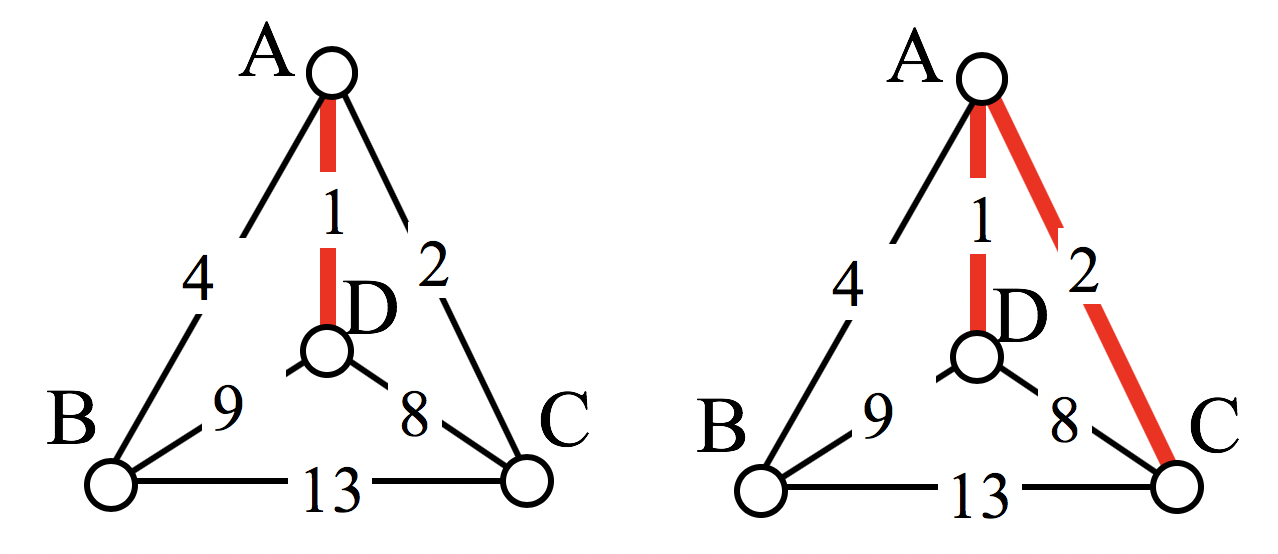
For the third edge, we’d like to add AB, but that would give vertex A degree 3, which is not allowed in a Hamiltonian circuit. The next shortest edge is CD, but that edge would create a circuit ACDA that does not include vertex B, so we reject that edge. The next shortest edge is BD, so we add that edge to the graph.
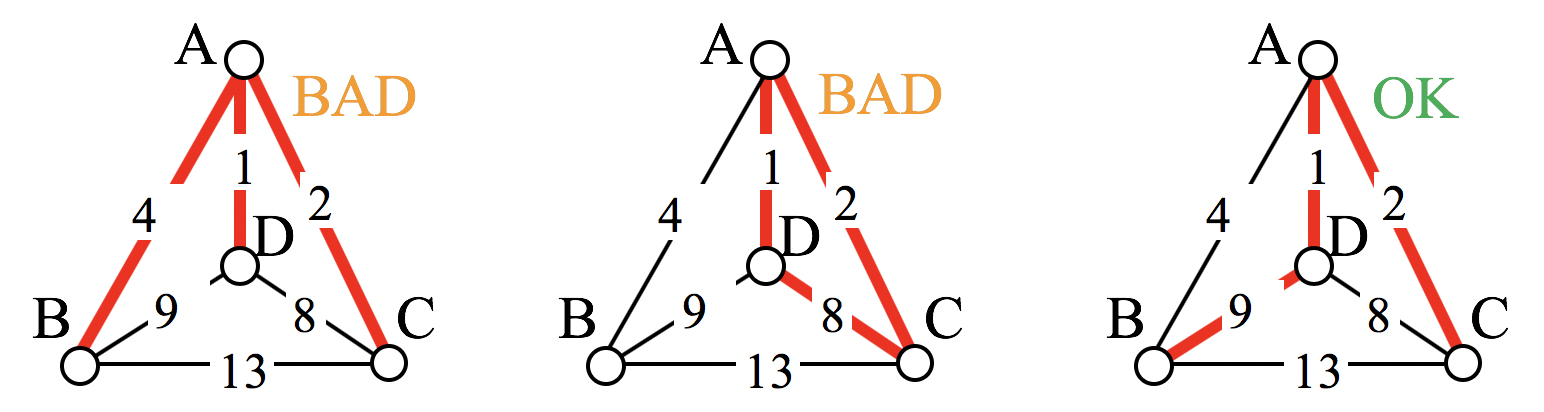
We then add the last edge to complete the circuit: ACBDA with weight 25.
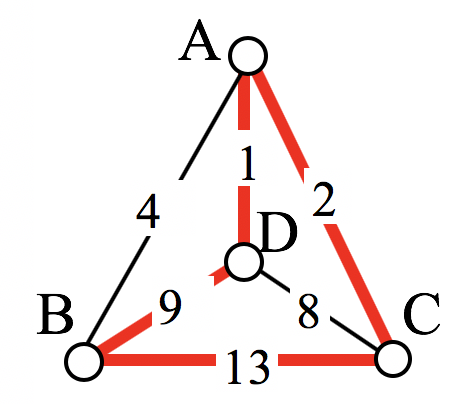
Notice that the algorithm did not produce the optimal circuit in this case; the optimal circuit is ACDBA with weight 23.
While the Sorted Edge algorithm overcomes some of the shortcomings of NNA, it is still only a heuristic algorithm, and does not guarantee the optimal circuit.
Find the circuit produced by the Sorted Edges algorithm using the graph below.
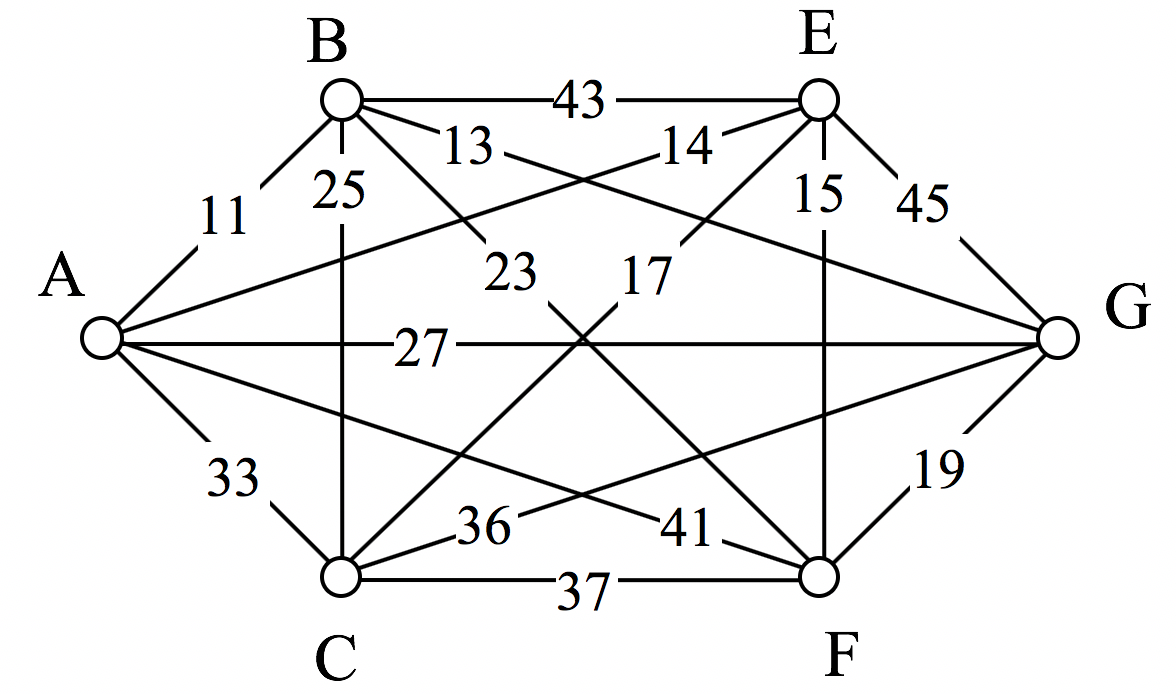
Use Nearest Neighbor and Sorted Edges to solve the Traveling Salesman problem on the graph below.
A company has 5 buildings. Costs (in thousands of dollars) to lay cables between pairs of buildings are shown below. Find the circuit that will minimize cost:

A company needs to deliver product to each of their 5 stores around the Dallas, TX area. Driving distances between the stores are shown below. Find a route for the driver to follow, returning to the distribution center in Fort Worth:
| Plano | Mesquite | Arlington | Denton | |
| Fort Worth | 54 | 52 | 19 | 42 |
| Plano | 38 | 53 | 41 | |
| Mesquite | 43 | 56 | ||
| Arlington | 50 |
A tourist wants to visit 7 cities in Israel. Driving distances, in kilometers, between the cities are shown below . Find a route for the person to follow, returning to the starting city:
| Jerusalem | Tel Aviv | Haifa | Tiberias | Beer Sheba | Eilat | |
| Jerusalem | ||||||
| Tel Aviv | 58 | |||||
| Haifa | 151 | 95 | ||||
| Tiberias | 152 | 134 | 69 | |||
| Beer Sheba |
81 | 105 | 197 | 233 | ||
| Eilat | 309 | 346 | 438 | 405 | 241 | |
| Nazareth | 131 | 102 | 35 | 29 | 207 | 488 |